Ja estamos na aula....

segunda-feira, 29 de março de 2010 às 07:46 | Postado por Educação Digital
Vamos atualizar nossos estudos, já estamos na Aula4 de trigonometria e Aula 8 de Pré-cálculo, não vamos deixar de estudar. Galera pode contar comigo.

| 0 comentários |

O que é matemática?

às 07:42 | Postado por Educação Digital
Números. Esses são instrumentos de trabalho de um matemático. Essa profissão é a ciência que estuda as relações lógicas e abstratas aplicadas aos símbolos. Relaciona o espaço e as quantidades. O profissional dessa área realiza testes de hipóteses e trabalha na formulação de teorias dentro dos diversos setores da ciência aplicada. Elabora banco de dados, a fim de desvendar e solucionar problemas de desenvolvimento de produtos, de produção e logística dentro de empresas de computação, de marketing, engenharia ou biologia. É possível trabalhar em áreas que lidam com pesquisas e dinheiro, como economia, finanças e física. Uma opção muito escolhida entre os profissionais brasileiros é a de professor, em ensino fundamental, médio ou superior.
Essa área está em um bom desenvolvimento no Brasil. Oportunidades surgem tanto para o bacharel quanto para o licenciado. O profissional com licenciatura é procurado, principalmente, em escolas públicas pelo país. Mas há vagas, também, em instituições particulares, no ensino fundamental, no médio e em cursinhos pré-universitários. O pós-graduado pode trabalhar em faculdades e universidades que possuem cursos na área de Exatas. Já em outros segmentos, os profissionais costumam ser procurados para exercerem funções do setor financeiro, como em bancos, por exemplo, ou de logística, em empresas de transporte. Empresas de informática e tecnologia da informação, indústrias e consultorias buscam matemáticos especialistas em modelagem.
Na universidade, o aluno estuda as teorias matemáticas e as inúmeras aplicações dessa matéria. Em média, são quatro anos. Nos dois primeiros, são estudados cálculo diferencial e integral, geometria, álgebra, estatística, probabilidade e informática. No ano seguinte, há opção para licenciatura, onde há aulas de pedagogia. Algumas instituições possuem nomes específicos para isso: Ciência (matemática) e Educação (ciências matemáticas). A outra opção é seguir o curso como bacharel com aprofundamento em matemática. Há cursos em que a aplicação segue para áreas específicas do conhecimento, como biologia, química, física, informática, computação ou economia

Posted In | 0 comentários |

Aula 01 Seno , Cosseno e Tangente.

quarta-feira, 3 de março de 2010 às 12:44 | Postado por Educação Digital

 

 
A partir deste triângulo retângulo obteremos todos os valores notáveis:
Seno de 30º = \frac{1}{2}; porque \frac{L}{2} (o cateto oposto) dividido pela Hipotenusa L resulta em \frac{1}{2}.
Cosseno de 30º = \frac{\sqrt{3}}{2}; porque o cateto adjacente dividido pela hipotenusa resulta nesse valor.
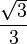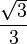Tangente de 30º = \frac{\sqrt{3}}{3}; Porque \frac{sen30}{cos30} = \frac{\frac{L}{2}}{\frac{L\sqrt{3}}{2}} resultando em \frac{\sqrt{3}}{3}.
De Maneira Análoga obtemos o Cosseno e o seno de 60º, utilizando a figura anterior.
- Obtendo os valores do ângulo de 45º.

Observando o quadrado abaixo, nota-se que ele foi dividido pela diagonal em dois triângulos retângulos com ângulos de 45º.
 

 No triângulo amarelo podemos descobrir o valor da hipotenusa, L\sqrt{2}.(e não dividido como na figura!)

 

Análise do ângulo C de 45 graus: O seno de 45 graus será o cateto oposto dividido pela hipotenusa resultando em \frac{1}{\sqrt{2}} que racionalizado fica \frac{\sqrt{2}}{2}, o mesmo ocorre com o cosseno, já a tangente é cateto oposto dividido pelo cateto adjacente que valem L resultando em \frac{L}{L}=1.

Algumas relações

\mbox{sen} A = {\mbox{cateto oposto} \over \mbox{hipotenusa}} \qquad \cos A = {\mbox{cateto adjaente} \over \mbox{hipotenusa}}
Estas são as mais importantes funções trigonométricas; outras funções podem ser definidas tomando as razões dos outros lados de um triângulo retângulo, mas podem ser expressas em termos de seno e cosseno. São elas a tangente, secante, cotangente, e cossecante.
\tan A = {\mbox{sen} A \over \cos A} = {\mbox{cateto oposto} \over \mbox{cateto adjacente}} \qquad \sec A = {1 \over \cos A} = {\mbox{hipotenusa} \over \mbox{cateto adjacente}}
\cot A = {\cos A \over \mbox{sen} A} = {\mbox{cateto adjacente} \over \mbox{cateto oposto}} \qquad \csc A = {1 \over \mbox{sen} A} = {\mbox{hipotenusa} \over \mbox{cateto oposto}}

 

Fórmula fundamental da trigonometria e seus corolários

\begin{align} \operatorname{sen}^2 A + \cos^2 A &= 1 \\ \tan^2 A + 1 &= \sec^2 A \\ 1+\cot^2 A &= \csc^2 A \end{align}

Identidades de soma e subtração

\begin{align} \mbox{sen}(A \pm B) &= \mbox{sen} A \cos B \pm \mbox{sen} B \cos A \\ \cos(A \pm B) &= \cos A \cos B \mp \mbox{sen} A \mbox{sen} B \\ \tan(A \pm B) &= \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B} \\ \cot(A \pm B) &= \frac{\cot A \ B \mp 1}{\cot B \pm \cot A} \end{align}

Fórmulas da duplicação do ângulo

\begin{align} \operatorname{sen}(2A)&= 2 \operatorname{sen} A \cos A \\ &= \frac{2 \tan A}{1 + \tan^2 A}\\ \cos(2A)&= \cos^2 A - \operatorname{sen}^2 A \\ &= 2 \cos^2 A -1 \\ &= 1-2 \operatorname{sen}^2 A \\ &= {1 - \tan^2 A \over 1 + \tan^2 A}\\ \tan(2A)&= \frac{2 \tan A}{1 - \tan^2 A}\\ &= \frac{2 \cot A}{\cot^2 A - 1}\\ &= \frac{2}{\cot A - \tan A} \end{align}

Fórmulas da divisão do ângulo em dois

Note que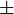 \pm está correto, isso significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.
\begin{align} \operatorname{sen} \frac{A}{2} &= \pm {\sqrt\frac{1-\cos A}{2}} \\ \cos \frac{A}{2} &= \pm {\sqrt\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} \end{align}

Posted In , , | 0 comentários |

Assinar: Postagens (Atom)

Acolhimento | Powered by Blogger | Entries (RSS) | Comments (RSS) | Designed by MB Web Design | XML Coded By Cahayabiru.com Distribuído por Templates