Aula 01 Seno , Cosseno e Tangente.

quarta-feira, 3 de março de 2010 às 12:44 | Postado por Educação Digital

 

 
A partir deste triângulo retângulo obteremos todos os valores notáveis:
Seno de 30º = \frac{1}{2}; porque \frac{L}{2} (o cateto oposto) dividido pela Hipotenusa L resulta em \frac{1}{2}.
Cosseno de 30º = \frac{\sqrt{3}}{2}; porque o cateto adjacente dividido pela hipotenusa resulta nesse valor.
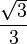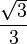Tangente de 30º = \frac{\sqrt{3}}{3}; Porque \frac{sen30}{cos30} = \frac{\frac{L}{2}}{\frac{L\sqrt{3}}{2}} resultando em \frac{\sqrt{3}}{3}.
De Maneira Análoga obtemos o Cosseno e o seno de 60º, utilizando a figura anterior.
- Obtendo os valores do ângulo de 45º.

Observando o quadrado abaixo, nota-se que ele foi dividido pela diagonal em dois triângulos retângulos com ângulos de 45º.
 

 No triângulo amarelo podemos descobrir o valor da hipotenusa, L\sqrt{2}.(e não dividido como na figura!)

 

Análise do ângulo C de 45 graus: O seno de 45 graus será o cateto oposto dividido pela hipotenusa resultando em \frac{1}{\sqrt{2}} que racionalizado fica \frac{\sqrt{2}}{2}, o mesmo ocorre com o cosseno, já a tangente é cateto oposto dividido pelo cateto adjacente que valem L resultando em \frac{L}{L}=1.

Algumas relações

\mbox{sen} A = {\mbox{cateto oposto} \over \mbox{hipotenusa}} \qquad \cos A = {\mbox{cateto adjaente} \over \mbox{hipotenusa}}
Estas são as mais importantes funções trigonométricas; outras funções podem ser definidas tomando as razões dos outros lados de um triângulo retângulo, mas podem ser expressas em termos de seno e cosseno. São elas a tangente, secante, cotangente, e cossecante.
\tan A = {\mbox{sen} A \over \cos A} = {\mbox{cateto oposto} \over \mbox{cateto adjacente}} \qquad \sec A = {1 \over \cos A} = {\mbox{hipotenusa} \over \mbox{cateto adjacente}}
\cot A = {\cos A \over \mbox{sen} A} = {\mbox{cateto adjacente} \over \mbox{cateto oposto}} \qquad \csc A = {1 \over \mbox{sen} A} = {\mbox{hipotenusa} \over \mbox{cateto oposto}}

 

Fórmula fundamental da trigonometria e seus corolários

\begin{align} \operatorname{sen}^2 A + \cos^2 A &= 1 \\ \tan^2 A + 1 &= \sec^2 A \\ 1+\cot^2 A &= \csc^2 A \end{align}

Identidades de soma e subtração

\begin{align} \mbox{sen}(A \pm B) &= \mbox{sen} A \cos B \pm \mbox{sen} B \cos A \\ \cos(A \pm B) &= \cos A \cos B \mp \mbox{sen} A \mbox{sen} B \\ \tan(A \pm B) &= \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B} \\ \cot(A \pm B) &= \frac{\cot A \ B \mp 1}{\cot B \pm \cot A} \end{align}

Fórmulas da duplicação do ângulo

\begin{align} \operatorname{sen}(2A)&= 2 \operatorname{sen} A \cos A \\ &= \frac{2 \tan A}{1 + \tan^2 A}\\ \cos(2A)&= \cos^2 A - \operatorname{sen}^2 A \\ &= 2 \cos^2 A -1 \\ &= 1-2 \operatorname{sen}^2 A \\ &= {1 - \tan^2 A \over 1 + \tan^2 A}\\ \tan(2A)&= \frac{2 \tan A}{1 - \tan^2 A}\\ &= \frac{2 \cot A}{\cot^2 A - 1}\\ &= \frac{2}{\cot A - \tan A} \end{align}

Fórmulas da divisão do ângulo em dois

Note que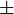 \pm está correto, isso significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.
\begin{align} \operatorname{sen} \frac{A}{2} &= \pm {\sqrt\frac{1-\cos A}{2}} \\ \cos \frac{A}{2} &= \pm {\sqrt\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} \end{align}

Posted In , , | |

Assinar: Postar comentários (Atom)

Acolhimento | Powered by Blogger | Entries (RSS) | Comments (RSS) | Designed by MB Web Design | XML Coded By Cahayabiru.com Distribuído por Templates